Stochastic Control with Signatures

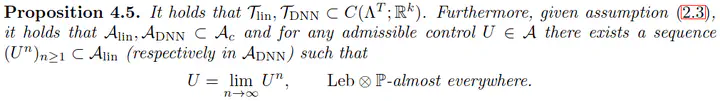
Abstract

This paper proposes to parameterize open loop controls in stochastic optimal control problems via suitable classes of functionals depending on the driver’s path signature, a concept adopted from rough path integration theory. We rigorously prove that these controls are dense in the class of progressively measurable controls and use rough path methods to establish suitable conditions for stability of the controlled dynamics and target functional. These results pave the way for Monte Carlo methods to stochastic optimal control for generic target functionals and dynamics. We discuss the rather versatile numerical algorithms for computing approximately optimal controls and verify their accurateness in benchmark problems from Mathematical Finance.

Tobias Christian Nauen

PhD Student

My research interests include efficiency of machine learning models, multimodal learning, and transformer models.